Is Kanye Zipfy?

I came across an interesting tool over the weekend. Kanye rest is a quick hack that a couple of students over in Manchester put together over a long weekend[1]. It's a fully Restful API that has some pretty interesting endpoints[1:1]. For example, the album endpoint returns the lyrics of a specified album:
http://www.kanyerest.xyz/api/album/the_life_of_pablo
Issuing a request on using the link returns the following output (scaled down for this post):
{
"result": [
{
"album": "the_life_of_pablo",
"lyrics": "...",
"title": "ultralight_beam"
},
{
"album": "the_life_of_pablo",
"lyrics": "...",
"title": "father_stretch_my_hands,_pt._1"
},
...
]
}
However, what I found most interesting was the counter endpoint:
http://www.kanyerest.xyz/api/counter
which the authors describe as:
This endpoint returns the count of each word used by King Kanye in all his songs. Ever.
{
...
"pull": 35,
"pulled": 10,
"pullin": 1,
"pulling": 1,
"pump": 8,
...
}
Given such a large set of data, the possibilities for analysis are endless. For example, sorting the words by frequency of occurrence reveals Kanye's top 10 most commonly used words to be:
1 i, 3001
2 the, 2921
3 you, 2273
4 to, 1577
5 and, 1423
6 a, 1415
7 it, 1062
8 my, 1032
9 me, 961
10 in, 930
To put this into context, the most common words in the English language[1:2] are:
1 the
2 be
3 to
4 of
5 and
6 a
7 in
8 that
9 have
10 I
While it is certainly of remarkable (although not completely unexpected) that his most commonly used word is I, a much bigger question would be;
Is Kanye West bound by Zipf's law?
Zipf's law[1:3] is discrete power law probability distribution that can be observed in natural language corpus. It formally states that,
\[f(k; s, N) = \frac{\frac{1}{k^{s}}}{\sum_{n=1}^N(\frac{1}{n^s})} \]
where,
Nis the number of elements;kis their rank;- and
sis the value of the exponent characterizing the distribution.
The frequency of any word is inversely proportional to its rank in the frequency table. Thus the most frequent word will occur approximately twice as often as the second most frequent word, three times as often as the third most frequent word, etc[1:4].
To put our data set to the test, we can plot our data set on a logarithmic scale.
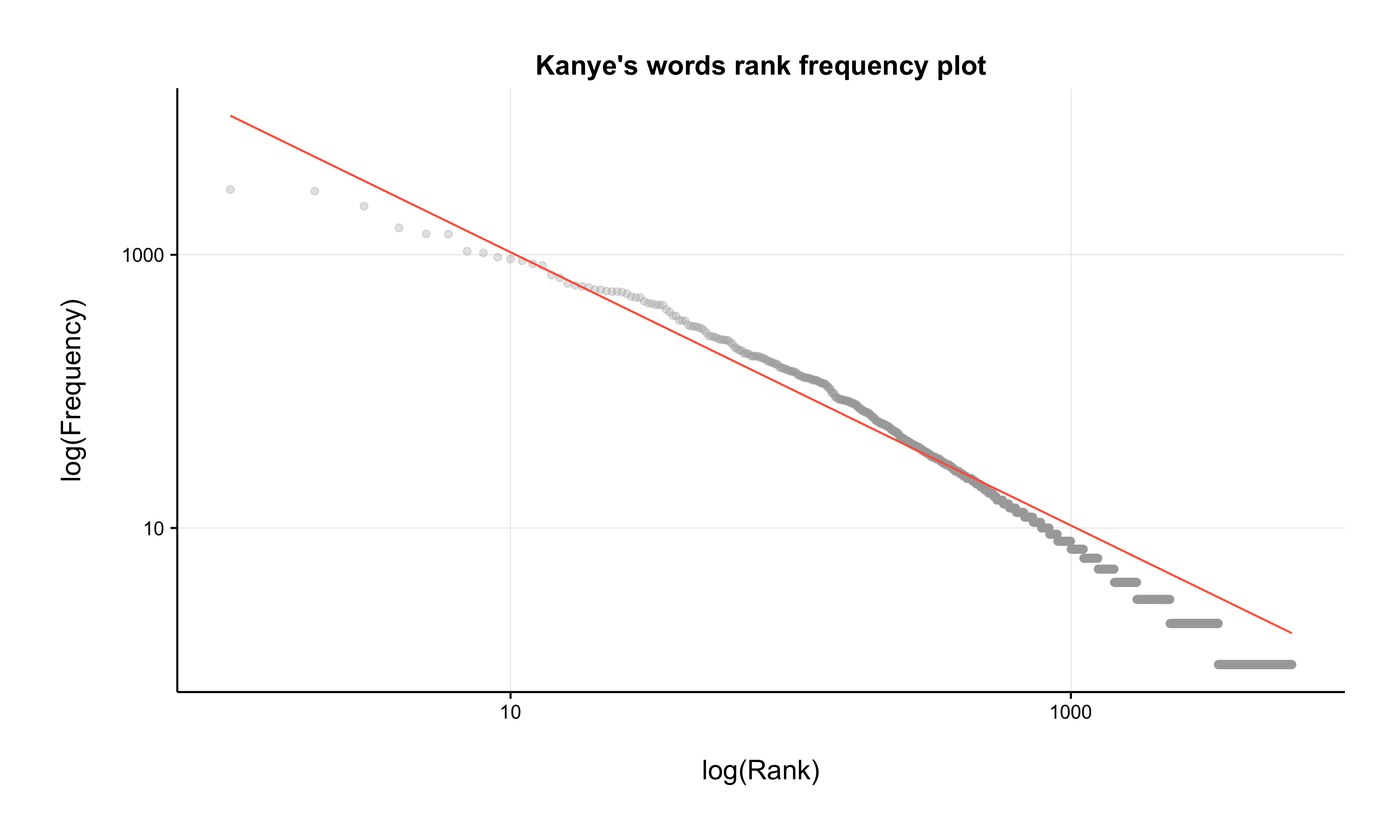
From the plot what's apparent (besides Kanye's rather surprising humility) is the trend towards the predicted Zipf's distribution for this data set. It also shows that he tends to use higher ranked words more often than expected. I speculate that this may be attributed to the nature of his art form; songs tend to repeat certain word groups a lot (Rihanna's recent single work[1:5] comes to mind).
Some other noteworthy statistics worth noting from further analyzing the data shows:
-
Kanye's top
10most used words account for20.6%of the dataset. -
His top
100most used words account for55.8%the dataset. -
The top
20%of words he uses account for89%of the data set; consistent with the Pareto principle[1:6].
Conclusion
While some may argue that Kanye's lyrics are incendiary, the analysis demonstrated above shows that they are not exempt from Zipf's law. While the distribution above loosely followed the predicted trend, there is a correlation. This could adjusted for through an application of the Zipf–Mandelbrot's[1:7] law.
As a topic of further research, it may be of interest to see if other artists follow similar trends and if there are variations across music genres. This could possibly be done by analyzing data obtained through a more comprehensive service such as the Genius API[1:8].